Observation of 2D-magnesium-intercalated gallium nitride superlattices
Thermal annealing of metallic Mg on GaN
This intercalation occurs at low cost and with accessible conditions, specifically the annealing of a bare metallic Mg film on GaN in either a nitrogen or argon atmosphere at atmospheric pressure. This process is characterized by a rapid diffusion that requires only a few minutes at temperatures in the range 550–800 °C, which is fully compatible with existing semiconductor fabrication processes.
We first deposited metallic Mg thin film, without a capping layer, onto single-crystalline wurtzite GaN (hexagonal P63mc space group) using conventional physical vapour-deposition methods, such as electron-beam evaporation or sputtering. Subsequently, these samples were then annealed at elevated temperatures in atmospheric pressure, typically exceeding 550 °C for 10 min. Notably, higher annealing temperatures corresponded to reduced times required for the intercalation process. When heated above the melting point of Mg (650 °C), molten Mg also proved effective in producing this effect. The rapid interstitial diffusion of Mg within GaN resulted in its segregation into single monolayer atomic sheets. These sheets then expanded in size, resembling climbing motion of edge dislocations, and aligned vertically (along the c axis) with each other in an even and orderly manner. However, given the spontaneous and diffusion-driven nature of this reaction, the nucleation of Mg intercalants within the GaN matrix tended to be inhomogeneous, leading to a non-uniform distribution of the resulting MiGs domains (Extended Data Fig. 1).
Atmospheric pressure is strongly recommended to prevent the early sublimation of Mg before it reacts with GaN. Because Mg evaporates easily at low pressure, for example in the high-vacuum condition in a typical molecular-beam epitaxy (MBE) growth environment (10−8 to 10−12 torr, which is roughly 10−6 to 10−10 Pa), the boiling point of Mg is below 200 °C51, whereas under 1 atmosphere, the boiling point of Mg increases to more than 1,000 °C, which is much higher than the melting point of 650 °C52. Therefore, if a 50-nm-thick Mg film is annealed in a rapid thermal annealing furnace at 700 °C under a vacuum of 10 Pa, given that the boiling point of Mg is approximately 500 °C, the Mg should have sublimated during the temperature ramp-up phase.
Before Mg deposition, if the GaN samples contain a top p-type GaN epitaxial layer that was initially doped with Mg during epitaxy, the samples were first subjected to a conventional annealing process (750 °C for 10 min) for Mg activation and hydrogen depassivation53.
We then deposited an amorphous, pure, bare metallic Mg thin film, approximately 50 nm thick, onto the GaN samples using an ACS-4000 (ULVAC) sputtering system with a 3 N (99.9% purity) Mg target.
After deposition, the handling of metallic Mg film requires special attention to prevent oxidation and dissolution during the lift-off process in liquids. Generally, the oxidation resistance of Mg is considered good in dry air up to approximately 400 °C, and up to about 350 °C in moist air, with humidity having an important role in Mg corrosion as it forms Mg(OH)2 (ref. 54). Based on our experience, at room temperature the oxidation resistance of Mg is robust; the as-deposited Mg thin film (50 nm) retains its metallic lustre when kept in air for days. We did not take special measures to prevent its oxidation, and the thermal annealing of the Mg film was typically conducted within one day after deposition. However, Mg is prone to oxidation in dry air above 500 °C, so pure nitrogen or argon is needed during annealing. Nonetheless, we acknowledge that the Mg film surface was probably oxidized and covered by a thin oxide layer as a result of its exposure to air. This might also explain the extra oxygen that was incorporated into the MiGs structure in the secondary ion mass spectrometry (SIMS) profiles (Supplementary Fig. 3).
For photolithography and patterning of Mg, the lift-off process of photoresist and Mg film was done in liquid solution. We found that Mg nanofilm tended to dissolve in deionized water, losing its metallic colour after just a few minutes, so we avoided using deionized water. Instead, we opted for pure isopropyl alcohol (IPA), finding that Mg remains stable in IPA, which is sufficient for the lift-off process. IPA is routinely used instead of deionized water in semiconductor processing practices. We also used N-methyl-2-pyrrolidone (or acetone) followed by methanol for the lift-off process before using IPA.
The GaN samples, after undergoing blank deposition or pattering of Mg film, were annealed at various temperatures: 500 °C, 550 °C, 600 °C, 700 °C and 800 °C, all for 10 min. Unless specified otherwise in comparative experiments for annealing temperature, we set the default annealing temperature at 800 °C. We found that the formation of superlattice structure was characterized by a rapid diffusion process that required only 10 min or less at temperatures ranging from 550 °C to 800 °C. Temperatures between 800 °C and 1,000 °C are feasible but made no substantial difference compared with temperatures of around 800 °C. However, annealing at temperatures higher than 1,000 °C requires a masking layer to prevent incongruent decomposition of GaN. Furthermore, annealing at temperatures of more than 1,000 °C favours substitutional diffusion of Mg55, which could lead to thermal instability of the superlattice structure and decomposition of the interstitial Mg sheets. Temperatures lower than 550 °C might be possible but could require much longer annealing times45.
After cooling, the samples were cleaned with either hydrochloric acid or aqua regia. This cleaning step was essential for removing any Mg residues and compounds that were soluble in acid, which might have formed during exposure to moisture, hot air or hot nitrogen.
Preparation of GaN samples
We used a diverse range of GaN samples to demonstrate the accessibility and versatility of the Mg intercalation process. Our findings indicate that, regarding the formation and morphology of the superlattice structure, there is no great difference between n-type GaN and p-type GaN, except for the initial Mg content in these samples. Specifically, n-type GaN does not contain Mg initially, whereas p-type GaN is already enriched with Mg. These pre-existing Mg atoms could contribute to the formation of Mg sheets. Consequently, the presence of Mg in p-type GaN may slightly lower the diffusion temperature or the time required to form the MiGs structure. Thus, including studies on both n-type and p-type GaN samples in our research may highlight the general applicability of this method, regardless of their conductivity type and film quality. As a result, our GaN samples varied in initial doping concentration (heavily n-doped, which is a commercial n-type GaN substrate without re-epitaxy, and lightly n-doped, which is unintentionally doped GaN, lightly p-doped and heavily p-doped) and substrate type (commercial GaN templates, consisting of GaN buffer layers on sapphire substrates, and commercial GaN substrates).
-
1.
For samples used for the HAADF-STEM and iDPC-STEM observations, except for the STEM observation with I–V characteristics in Fig. 4, the unintentionally doped GaN 2 µm thick was grown by metal–organic vapour phase epitaxy on a commercial (0001) heavily doped n-type GaN substrate 400 μm thick and 2 inches (51 mm) in diameter with a free electron concentration of around 1018 cm−3.
-
2.
For samples used for the STEM-cathodoluminescence (CL) characterizations, these GaN substrates with epitaxy-ready smoothness were used.
-
3.
For GaN samples used for plan-view CL and cross-sectional polarized CL measurements, we used epitaxy layers consisting of 200-nm-thick p-type GaN with [Mg] = 6 × 1018 cm−3 followed by 1-μm-thick unintentionally doped GaN on the above-mentioned GaN substrate.
-
4.
For GaN samples used for terahertz time-domain ellipsometry, the epitaxy layers consisted of p-type GaN around 450 nm thick, one with [Mg] = 6 × 1018 cm−3 and another with [Mg] = 2 × 1019 cm−3, followed by 3.9-μm-thick unintentionally doped GaN ([C] = 2 × 1016 cm−3, [O] = 1 × 1016 cm−3 and [Si] below the detection limit) on commercial sapphire substrates 2 inches in diameter. We also prepared another GaN sample with the same 3.9-μm-thick unintentionally doped GaN (without p-type GaN) on the above-mentioned sapphire substrate and a bare sapphire substrate.
-
5.
For GaN samples used for C–V profiling, the epitaxy layers consisted of unintentionally doped GaN roughly 2 μm thick with a net doping concentration of 6 × 1016 cm−3 on the above-mentioned GaN substrate.
-
6.
For GaN samples used for backside secondary-ion mass spectrometry (SIMS), the epi-layers consisted of 400-nm-thick p-type GaN ([Mg] = 7 × 1018 cm−3) and 2.5-μm-thick unintentionally doped GaN with [Si] = 7 × 1016 cm−3 on the above-mentioned GaN substrate.
-
7.
For GaN samples used for I–V characteristics and the combined STEM observations, the samples were the same with those in item (6). The conventional top degenerately doped p-type contact layer (the p+ contact layer) intended for ohmic contact purposes was not grown intentionally.
STEM-based characterizations
STEM samples were prepared using a Thermo Fisher Helios 660 focused ion beam (FIB) STEM. Before FIB sample preparation, a protective carbon layer was deposited on the sample surface to reduce Ga FIB-induced damage. Samples were thinned with starting and final energies of 30 kV and 1 kV, respectively. The resulting lamellae were less than 50 nm thick. HAADF-STEM imaging was performed on a probe corrected Hitachi HD 2700 STEM operated at 200 kV with a convergence semi-angle of 23.5 mrad.
The iDPC-STEM imaging was performed on a probe corrected Thermo Fisher Themis 80-300 kV STEM operated at 200 kV with a convergence semi-angle of 25.3 mrad using a four-quadrant DF4 detector56.
For the elemental EDS maps of Ga, N and Mg, the measurements were taken using a Thermo Fisher Super-X system in the same STEM set-up as that used for the iDPC data. The Super-X system consists of four silicon drift detectors for improved X-ray collection efficiency and offers good sensitivity and high spatial resolution capability. A radial Wiener filter was used for the elemental EDS maps of Ga, N and Mg.
STEM-CL characterization involved sample preparation by FIB using a Thermo Fisher Scientific Helios 660 with lamella specimens approximately 500 nm thick. The STEM-CL measurements were done on a JEOL JEM-2100 F analytical electron microscope at an acceleration voltage of 120 kV and a beam diameter of 1.0 nm. High-resolution STEM observations associated with the STEM-CL measurements were performed on a JEOL JEM-ARM200F analytical electron microscope at an acceleration voltage of 200 kV and a beam diameter of 0.15 nm.
Strain determination
For the in-plane and out-of-plane strains, they are defined by the following formulas, respectively:
$${\varepsilon }_{a}( \% )=\frac{{a}_{{\rm{s}}}-{a}_{{\rm{r}}}}{{a}_{{\rm{r}}}}\times 100$$
(2)
$${\varepsilon }_{c}( \% )=\frac{{c}_{{\rm{s}}}-{c}_{{\rm{r}}}}{{c}_{{\rm{r}}}}\times 100$$
(3)
where the subscript s refers to GaN in the strain-mapping region (GaN between periodic 2D-Mgi sheets excluding the tip region) and the subscript r denotes GaN in the reference region (outside the intercalation region). The terms a and c represent the in-plane and out-of-plane lattice constants of hexagonal GaN, respectively. These constants are obtained on the basis of the measured average distance from atom column to atom column. The average in-plane distance, din-plane, and out-of-plane distance, dout-of-plane, have the following relationship with the lattice constants in a hexagonal lattice:
$${d}_{{\rm{out}} \mbox{-} {\rm{of}} \mbox{-} {\rm{plane}}}=\frac{1}{2}c$$
(4)
$${d}_{{\rm{in}} \mbox{-} {\rm{plane}}}=\frac{\sqrt{3}}{2}a$$
(5)
The direction of the in-plane strain is parallel to the m axis (the \( < 1\bar{1}00 > \) direction) and also equivalently to the a axis (the \( < 11\bar{2}0 > \) direction) in this work, owing to the symmetry of strain produced by the Mg sheets parallel to both the m axis and the a axis. The direction of out-of-plane strain is parallel to the c axis (the <0001> direction). The directions of the m, a and c axes are indicated in the lower left corner of Fig. 3b. When GaN is uniaxially strained along the c axis, the Poisson ratio, ν, is defined as:
$$\nu =-\frac{{\varepsilon }_{\perp }}{{\varepsilon }_{\parallel }}=-\frac{{\varepsilon }_{a}}{{\varepsilon }_{c}}$$
(6)
For atom-column by atom-column distance measurements, images were acquired using a frame-averaging approach to limit the effects of sample drift. Each frame-averaged dataset consisted of a minimum of 12 individual images that were then position-corrected using cross-correlation and averaged for the final image. To further limit the effects of drift, frame-averaged image series were acquired with the fast scan direction parallel to the measurement direction. The atom-column by atom-column measurements were performed by fitting each atom column position to a two-dimensional Gaussian distribution and measuring the distance between columns directly using the Atomap software package57.
Electronic band-structure calculation
The electronic band structures of GaN were calculated according to density functional theory (DFT) using the Vienna ab initio Simulation Package. The nuclei and core electrons were simulated by pseudopotentials generated by the projector-augmented-wave method. The exchange-correlation energy was treated in the generalized gradient approximation using the Perdew–Burke–Ernzerhof functional. In the electronic-structure calculations with the Heyd–Scuseria–Ernzerhof hybrid functional, the exact exchange amount was set to 26%, yielding a bandgap of 3.4 eV for unstrained wurtzite GaN, which aligns well with the experimental value for bulk GaN.
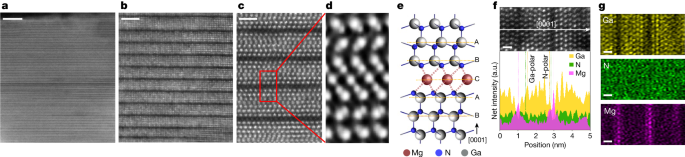
DFT simulations were not performed on the broader GaN and Mg superlattice for two main reasons. First, the MiGs structure, like the Guinier–Preston zone, is categorized as a structure rather than a compound material, the latter being exemplified by MAX phases. The non-stoichiometry of a structure greatly increases the computational expense of the relevant calculations. Merely constructing an Mg sheet, as depicted in Fig. 1e, would suggest that Mg sheets extend throughout the entire layer, which would result in substitutional rather than interstitial intercalation. Consequently, to honour the characteristic of interstitial intercalation, the Mg sheets must terminate within the GaN matrix. This necessitates a supercell comprising hundreds of atoms at least. Second, the gradual transition of polarity in the GaN lattice, as illustrated in Fig. 2f, substantially complicates the construction of a supercell model that properly reflects the unique features of such a structure. As such, DFT simulations on the GaN and Mg superlattice may require much more effort in future studies.
Scanning electron microscopy (SEM)-CL mapping and polarization-resolved CL spectroscopy
SEM-CL was performed on an Allalin spectroscopic (analytical) platform from Attolight. A focused electron beam scanned the sample with normal incidence and the optical emission was collected. Angles rotationally symmetric between 18° and 46° from the incident beam were captured. The optical beam was then analysed by using a spectrometer to obtain a luminescence spectrum for each pixel of the image. The optical analysis apparatus consisted of a monochromator fitted with a 1,024×256 charge-coupled device high-speed camera adapted for ultraviolet-visible detection (wavelengths of 200–1,100 nm). The camera enabled almost-instant acquisition of the entire emission spectrum. The samples were measured in both plan and cross-sectional views (for polarization-resolved CL only) at room temperature. The voltage of the incident electron beam was set to 10 kV. The scans were square and their size varied from 5 μm to 50 μm, depending on the width of the measured line on the sample, and the number of data points was kept at 128×128. The integration time at each pixel was set to 10 ms, resulting in a total acquisition time for one image of 165 s. Acquired luminescence spectra resulted from electronic transitions around the bandgap of GaN. After acquisition, the spectrum at each pixel was approximatively fitted with a Gaussian curve. Peak energy was determined from the Gaussian centre.
THz-TDE
Free carrier absorption exists in the terahertz region, which allows the characterization of electrical conductivity58. This method is preferred to the conventional van der Pauw method because the latter only measures sheet resistivity (the inverse of in-plane conductivity, σ⊥), whereas THz-TDE encompasses both in-plane (σ⊥) and out-of-plane (σ∥) components59.
Our THz-TDE was performed using the Tera Evaluator, a commercial terahertz time-domain ellipsometer from Nippo Precision, with a reliable spectral range of 1.0–2.5 THz. The angle of incidence was fixed at 70° (ref. 58). To characterize the change in polarization of the terahertz waves after reflection on the sample, the ellipsometric parameters, namely amplitude ratio (tan Ψ) and phase difference (Δ) between the p and s polarization components, were measured59.
These ellipsometric parameters were initially measured from a bare sapphire substrate. This was followed by measurements on a 3.99-μm-thick unintentionally doped (lightly n-doped) GaN on the aforementioned sapphire substrate, and measurements of three 430-nm-thick p-type/3.99-μm-thick unintentionally doped (lightly n-doped) GaN/sapphire samples (one of them has incorporated MiGs nanostructures, formed by annealing of 50 nm metallic Mg film onto the entire GaN at 800 °C and 10 min). Three p-type GaN samples formed two control groups: the first consisted of p-type GaN samples with varying initial Mg doping concentrations (7 × 1018 cm−3 and 2 × 1019 cm−3); the second comprised the lower-Mg-doped p-type GaN samples, with and without MiGs phases, named samples 1 and 2, respectively. The higher-Mg-doped GaN sample without MiGs phases was known as sample 3 (Extended Data Fig. 6a).
During measurements, the equipment chamber was purged with dry air to minimize terahertz absorption by water vapour, and the ambient temperature was maintained at 22 °C. The terahertz spot size on the sample surface is 10 mm for the major diameter and 3 mm for the minor diameter. For the analysis, a three-layer optical model, approximating the sample structure, was constructed. This model was then used to calculate the predicted response on the basis of Fresnel equations, which describe the light reflection at the interface between each layer, taking into account thickness and optical constants. The calculated values were subsequently compared with the experimental data, and the solution was optimized using regression analysis.
In the MiGs-incorporated p-type GaN epilayer, the measured optical and transport properties represent a composite of both p-type GaN and the MiGs phase. Fitting the conductivity spectra to the Drude model reveals the inverse of scattering time at the crossing point of the σ′ and σ″ curves (Extended Data Fig. 6e). Sample 3 had a shorter scattering time, τ, and higher conductivity, σ, consistent with its higher ionized impurity concentration. However, the scattering time for sample 2 was similar to that of sample 1. The sheet resistivity and hole concentration for these samples, also measured by the van der Pauw method, are summarized in Extended Data Fig. 6i for comparison. We observed that the resistivity measured by THz-TDE, denoted as ρDC, of sample 1 and sample 3 closely aligns with their sheet resistivity measured using the van der Pauw method, validating the optical model used in our THz-TDE analysis. By contrast, sample 2 exhibits a substantial decrease in ρDC compared with its sheet resistivity. The six-fold conductivity increase suggests there are important factors beyond the increased hole concentration, minor changes in the dielectric constant and surface roughness. Given the consistent scattering time in samples 1 and 2, it implies that sample 2 has greatly enhanced out-of-plane mobility, potentially resulting from a reduced effective mass from the predominance of split-off holes along the c axis.
Based on the Drude model, in which conductivity (σ) is proportional to carrier concentration and scattering time (τ) and inversely proportional to effective mass, our preliminary estimates (using data from Extended Data Fig. 6i) indicate that the average effective mass of holes in sample 2 is reduced to approximately 30% of that in sample 1.
For more specific details, in THz-TDE, p– and s-polarized terahertz waves were irradiated onto a sample at an oblique angle, and the physical properties of the sample are derived from the change in the polarization state of terahertz waves on reflection. The measured values (tan Ψ and Δ) are defined from the ratio of the reflection coefficients for p and s polarizations, \({\widetilde{r}}_{p}\) and \({\widetilde{r}}_{s}\):
$$\mathop{\rho }\limits^{ \sim }=\,\tan \,\varPsi \exp i\varDelta =\frac{{\mathop{r}\limits^{ \sim }}_{p}}{{\mathop{r}\limits^{ \sim }}_{s}}=\left(\frac{{\mathop{E}\limits^{ \sim }}_{r,p}}{{\mathop{E}\limits^{ \sim }}_{i,p}}\right)/\left(\frac{{\mathop{E}\limits^{ \sim }}_{r,s}}{{\mathop{E}\limits^{ \sim }}_{i,s}}\right)$$
(7)
where \({\widetilde{E}}_{r}\) and \({\widetilde{E}}_{i}\) represent the reflected and incident electric fields, respectively. In the measurement, the incident field is oriented such that \({\widetilde{E}}_{i,p}={\widetilde{E}}_{i,s}\). Hence, equation (7) can be simplified to \(\mathop{\rho }\limits^{ \sim }=\tan \,\varPsi \exp i\varDelta ={\mathop{E}\limits^{ \sim }}_{r,p}/{\mathop{E}\limits^{ \sim }}_{r,s}\), and it follows that
$$\tan \,\varPsi =\frac{|{\mathop{E}\limits^{ \sim }}_{r,p}|}{|{\mathop{E}\limits^{ \sim }}_{r,s}|}\hspace{2.22144pt}{\rm{a}}{\rm{n}}{\rm{d}}\,\varDelta ={\delta }_{r,p}-{\delta }_{r,s}$$
(8)
where δ represents phase. Therefore, tan Ψ and Δ represent the amplitude ratio and phase difference, respectively, between the p and s polarizations. These parameters are referred to as ellipsometric parameters.
The reflection coefficients for p and s polarizations are described by Fresnel equations:
$$\begin{array}{c}{\widetilde{r}}_{jk,p}=\frac{{\widetilde{n}}_{k}\cos {\theta }_{j}-{\widetilde{n}}_{j}\cos {\theta }_{k}}{{\widetilde{n}}_{k}\cos {\theta }_{j}+{\widetilde{n}}_{j}\cos {\theta }_{k}}\,\\ {\widetilde{r}}_{jk,s}=\frac{{\widetilde{n}}_{j}\cos {\theta }_{j}-{\widetilde{n}}_{k}\cos {\theta }_{k}}{{\widetilde{n}}_{j}\cos {\theta }_{j}+{\widetilde{n}}_{k}\cos {\theta }_{k}}\end{array}$$
(9)
where the subscripts j and k represent the media of light propagation, \(\widetilde{n}\) is the complex refractive index expressed by \(\widetilde{n}=n-i\kappa \), θj is the angle of incidence and θk is the transmission angle, which can be calculated using Snell’s law.
For a bulk sample that consists of only a single layer, the complex refractive index can be obtained directly from the measured ellipsometric parameters:
$${\widetilde{n}}_{1}={\widetilde{n}}_{0}\,\sin {\theta }_{0}\sqrt{{\left(\frac{1-\widetilde{\rho }}{1+\widetilde{\rho }}\right)}^{2}{\tan }^{2}{\theta }_{0}+1}$$
(10)
where \({\widetilde{n}}_{0}\) is the complex refractive index of the ambient (air) and θ0 is the angle of incidence.
For a thin film/substrate structure, the complex refractive index of the film can be obtained numerically using the following expression:
$$\widetilde{\rho }=\frac{{\widetilde{r}}_{p}}{{\widetilde{r}}_{s}}=\left[\frac{{\widetilde{r}}_{01,p}+{\widetilde{r}}_{12,p}\exp (-i2\beta )}{1+{\widetilde{r}}_{01,p}{\widetilde{r}}_{12,p}\exp (-i2\beta )}\right]/\left[\frac{{\widetilde{r}}_{01,s}+{\widetilde{r}}_{12,s}\exp (-i2\beta )}{1+{\widetilde{r}}_{01,s}{\widetilde{r}}_{12,s}\exp (-i2\beta )}\right]$$
(11)
where β represents the film phase thickness given by \(\beta =2{\rm{\pi }}d{\widetilde{n}}_{1}\cos {\theta }_{1}/\lambda \), λ is the wavelength and d is the film thickness.
For a three-layer sample structure, the ellipsometric parameter can be expressed as:
$$\begin{array}{c}\mathop{\rho }\limits^{ \sim }=\frac{{\mathop{r}\limits^{ \sim }}_{p}}{{\mathop{r}\limits^{ \sim }}_{s}}=\left[\frac{{\mathop{r}\limits^{ \sim }}_{01,p}+{\mathop{r}\limits^{ \sim }}_{123,p}\exp (-i2{\beta }_{1})}{1+{\mathop{r}\limits^{ \sim }}_{01,p}{\mathop{r}\limits^{ \sim }}_{123,p}\exp (-i2{\beta }_{1})}\right]\,/\,\left[\frac{{\mathop{r}\limits^{ \sim }}_{01,s}+{\mathop{r}\limits^{ \sim }}_{123,s}\exp (-i2{\beta }_{1})}{1+{\mathop{r}\limits^{ \sim }}_{01,s}{\mathop{r}\limits^{ \sim }}_{123,s}\exp (-i2{\beta }_{1})}\right]\\ \,=\,\tan \,\varPsi \exp i\varDelta \end{array}$$
(12)
where \({\widetilde{r}}_{01}\) represents the reflection coefficient for the ambient–first layer interface and \({\widetilde{r}}_{123}\) is the reflection coefficient for the second layer and substrate, and is in turn given by
$${\widetilde{r}}_{123}=\frac{{\widetilde{r}}_{12}+{\widetilde{r}}_{23}\exp (-i2{\beta }_{2})}{1+{\widetilde{r}}_{12}{\widetilde{r}}_{23}\exp (-i2{\beta }_{2})}$$
(13)
The measured ellipsometric parameters for the sapphire substrate and n-type GaN/sapphire sample are shown in Extended Data Fig. 6f. Using equations (10) and (11), the complex refractive index of sapphire and of the n-type GaN film were obtained, respectively, as shown in Extended Data Fig. 6g. The extinction coefficient of the n-type GaN film shows an increasing trend towards low frequencies, which can be attributed to free carrier absorption. Extended Data Fig. 6h shows the complex refractive-index spectra obtained for the p-type GaN layers in the p-GaN/n-GaN/sapphire samples using equation (12). The spectra are fitted to the Drude model. In these measurements, the optic axis of the samples is normal to the surface.
It is important to note that the optical constants were calculated under the assumption of an isotropic model, despite GaN being a uniaxial crystal. Thus, the solutions are only an approximation of the dielectric function and do not represent exact optical constants, although they can be more appropriately regarded as pseudo-dielectric functions. Regardless, they provide insights into the differences between the optical responses of samples with and without MiGs phases and offer semi-quantitative evidence of an enhancement in conductivity in Mg-intercalated GaN.
Van der Pauw method
After the THz-TDE measurements, Hall-effect measurements (the van der Pauw method) at room temperature were performed on the above-mentioned p-type GaN samples (ResiTest8400 system) using a magnetic field with an amplitude of 0.5 T. The samples were diced into small pieces and the van der Pauw pattern for each measurement consisted of 1.5 mm × 1.5 mm. Ni/Au electrodes were formed by electron-beam evaporation. The contact metal was annealed at 525 °C for 5 min in O2 ambient to reduce the contact resistance.
SIMS
SIMS was performed at Eurofins EAG Laboratories. For backside SIMS measurement, samples were first polished and thinned to approximately 1 μm before being sputtered from the backside. Cs+ and O− primary ion beams were used to detect negative secondary ions (from C, H, O and Si) and positive secondary ions (Mg), respectively.
Electrical characterizations
For C–V profiling, Ni (70 nm)/Au (70 nm) stacks were electron-beam evaporated to form circular Schottky-contact electrodes (around 220 µm in diameter) without sintering. A shadow mask was used for patterning, chosen over photolithography to prevent potential damage from developing agents to the sample surface. Ti (20 nm)/Au (100 nm) stacks were electron-beam evaporated on the backside of the n-type GaN substrates for ohmic contact without sintering. All C–V measurements were performed at a frequency of 100 kHz using an E4980A LCR meter by Agilent.
For measurement of I–V characteristics combined with STEM observations, the samples were prepared with half of the region blank deposited with Mg and the other half was patterned with Mg using maskless photolithography (Nanosystem Solutions DL-1000). After this, the samples underwent the previously mentioned annealing process and were subsequently cleaned with acid. In the next step, using maskless photolithography, Ni (20 nm)/Au (150 nm) was electron-beam evaporated onto regions approximately identical to those where Mg had previously been deposited. This was done with the aid of alignment photolithography, achieving a precision of around 2 μm, to ensure the absence of Mg in the regions between the Ni/Au electrodes. Finally, sintering was carried out at 525 °C for 5 min in an O2 atmosphere to form the ohmic contact. After this, the samples were diced such that the half entirely covered with Mg-annealed surface was designated for STEM observations, whereas the other half, with selectively patterned Mg, was used for evaluating ohmic contact resistance through I–V characterization. An Agilent B1505A analyser was used to measure I–V characteristics in this work.








